par Alain Costé, université de Caen Normandie, Laboratoire de Mathématiques Nicolas Oresme (LMNO)
Article publié dans le Bulletin de la Société historique de Lisieux (ISSN 1164-7582) Fascicule 37, Janvier 1997.
L’homme et l’écrivain
Nicole Oresme est un des plus grands penseurs du XIVe siècle. Son œuvre philosophique est fondée sur un savoir étendu qui va de l’économie politique à la théologie en passant par les mathématiques, la physique, l’astronomie, la morale, l’économie et la politique. Il apparaît comme précurseur dans beaucoup de domaines. Il a eu aussi le grand mérite d’avoir mis le savoir scolastique à la portée d’un large public en traduisant en français plusieurs textes d’Aristote et en donnant des versions françaises de certaines de ses propres œuvres. Ce travail nouveau pour l’époque a été d’autant plus important qu’il a certainement joué un rôle dans le développement de la langue française.
Nicole Oresme est né vers 1320 dans le village d’Allemagne (Fleury sur Orne), près de Caen. En 1348 il est admis au collège de Navarre, fondé en 1304 par Jeanne, comtesse de Champagne, reine de Navarre et femme de Philippe le bel. Ce collège était établi sur le haut de la montagne Sainte Geneviève, là ou s’élève l’ancienne école Polytechnique. Il était ouvert sans condition de naissance, de famille ou d’âge, à tout français pauvre qui se destinait à l’étude de la grammaire, de la logique ou de la théologie. Nicole Oresme y reste treize ans et s’y distingue très vite; étudiant puis maître en divinité, il devient grand-maître le 4 Octobre 1356.
Pendant qu’il remplissait au collège ses diverses fonctions, il publie des oeuvres sur l’astrologie, la théologie, les mathématiques. Ces travaux sont rédigés en latin, puisque le latin est la langue parlée et écrite dans les collèges. C’est son traité des monnaies qui lui vaut d’attirer l’attention du dauphin Charles V beaucoup plus ouvert que son père Jean II le bon à la réflexion rationnelle et morale. Ainsi le philosophe va devenir un protégé de Charles V et entrer dans une nouvelle carrière. En 1362 il bénéficie de prébendes au chapitre de Rouen et devient doyen du chapitre en 1364. Il séjourne à Rouen, mais en même temps fréquente la cour, il a le titre de secrétaire du roi puis de conseiller et de chapelain. C’est durant cette dernière partie de sa vie qu’Oresme écrit ses œuvres en français et publie ses traductions commentées des livres d’Aristote. Il est sacré évêque de Lisieux le 28 janvier 1378. Charles V assiste à la cérémonie et lui offre deux anneaux d’or. Nicole Oresme s’installe à Lisieux à partir de juin 1378. Il meurt à Lisieux le 11 juillet 1382. Son corps est déposé dans la cathédrale, près de la porte gauche du chœur.
Œuvres en latin
Dans ce chapitre nous présentons les deux œuvres majeures de Nicole Oresme en mathématique et en physique, en mettant en exergue les points qui nous ont paru les plus marquants dans l’évolution de ces sciences.
Tractatus de configurationibus qualitatum et motum (Traité sur la configuration des qualités et du mouvement)
C’est dans ce traité que Nicole Oresme expose sa méthode de représentation graphique des variations d’une grandeur (qu’il appelle qualité) en fonction d’une autre grandeur. Il considère par exemple un corps dont la chaleur n’est pas homogène mais varie suivant l’endroit où on la mesure. Afin de représenter les variations de la chaleur au sein du corps, il imagine une droite tracée dans ce corps. Il appelle longitudino la longueur qui sépare un point courant de la droite à un point origine arbitrairement fixé. En chaque point de cette droite il élève une perpendiculaire dont la hauteur (latitudino) est proportionnelle à l’intensité de la chaleur au point correspondant du corps. Il obtient ainsi une figure géométrique dont l’examen rend plus aisé l’étude des variations de la chaleur. «Les propriétés de cette qualité, écrit-il, en seront examinées plus clairement et plus facilement dès lors que quelque chose qui lui est semblable est dessiné en une figure plane, et que cette chose, rendue claire par exemple visible, est saisie rapidement et parfaitement par imagination …car l’imagination des figures aide grandement à la connaissance des choses même»
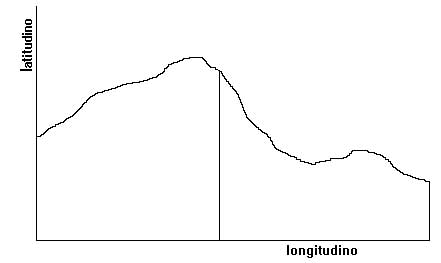
Il se livre ensuite à une étude mathématique des figures planes que produisent les représentations graphiques des qualités. Il leur fait subir des transformations géométriques simples en cherchant des propriétés invariantes, ce qui le conduit à une classification des courbes. On assiste là aux premiers balbutiements de la géométrie analytique. C’est en cela que d’aucuns considèrent Nicole Oresme comme précurseur de Descartes.
Mais notre auteur ne s’arrête pas à une étude purement abstraite. Il prétend donner des applications pratiques à sa doctrine de configuration dans des domaines variés. D’abord à la biologie; il affirme par exemple que la chaleur naturelle d’un lion agit de manière différente que celle d’un âne ou d’un bœuf. «Elle lui confère une puissance plus grande, non seulement parce qu’elle est plus intense, mais aussi parce que sa représentation graphique est dissemblable.» Plus loin il suggère que la configuration de la chaleur associée à la semence d’un homme joue un rôle essentiel dans la conception d’un bébé, la nature étant seule capable de produire cette configuration dans l’utérus d’une femme.
La doctrine de configuration est aussi présentée comme pouvant fournir une explication à ce pourquoi certaines pierres précieuses ou autres choses peuvent produire des effets curatifs. «La cause en est dans la similarité entre la configuration de la qualité de la pierre et la qualité corporelle de la personne qui est affectée… Ainsi à cause de la nature cachée de ces rapports certains nécromanciers stupides disent que ces propriétés curatives sont le résultat de la présence de certains esprits qu’ils ont introduits à l’intérieur.» Plus loin il tente de trouver des liens entre la doctrine de configuration et l’esthétique. Il y a-t-il une beauté absolue qui puisse être caractérisée par des rapports universels entre les configurations des qualités des choses ?
Toutes ces idées restent cependant essentiellement spéculatives. Sa tentative était grandement prématurée, et il l’a compris, la physique qu’il rêvait, il n’a pas vraiment cherché à la réaliser. C’est un document singulièrement significatif de l’esprit qui régnait, à la fin du XIVème siècle, dans les écoles de Paris, on était las des vertus occultes, on aspirait à une science rationnelle dont les explications invoqueraient seulement un petit nombre de propriétés élémentaires et se développeraient suivant les méthodes claires et sûres des mathématiques.
C’est dans le second volet de cet ouvrage, lorsqu’il applique la doctrine de configuration à l’étude du mouvement, que Nicole Oresme donne toute la mesure de son génie. C’est la partie de son oeuvre qui exerça une influence durable sur ses contemporains et qui sans nul doute a marqué l’histoire de la science du mouvement, à savoir la cinématique.
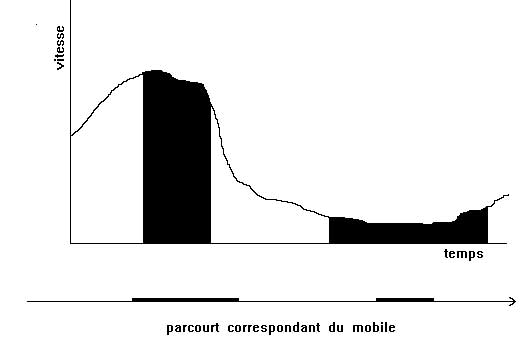
Afin de décrire et d’étudier un mouvement rectiligne, Nicole Oresme a l’idée de représenter graphiquement la vitesse instantanée du mobile en fonction du temps. Sur une droite horizontale il porte des graduations proportionnelles au temps et au dessus de chaque graduation il élève une perpendiculaire dont la longueur est proportionnelle à la vitesse du mobile à l’instant correspondant. Ce qui intéresse Nicole Oresme dans cette construction, c’est la portion de plan balayée par ces perpendiculaires successives. Par l’examen de cas particuliers simples et en généralisant, il aboutit à la conclusion que l’aire de la surface balayée par les perpendiculaires élevées au dessus de chaque graduation d’un intervalle de temps donné est proportionnelle à la distance parcourue par le mobile pendant cet intervalle de temps:
Ce postulat est à la base de ses découvertes relatives au mouvement uniformément accéléré. Voici .les grandes lignes de son raisonnement. Dans un mouvement rectiligne uniformément accéléré, l’accroissement de la vitesse du mobile est proportionnelle à la durée pendant laquelle se produit cet accroissement. La représentation graphique de la vitesse en fonction du temps décrite précédemment conduit alors à une figure en forme de trapèze:
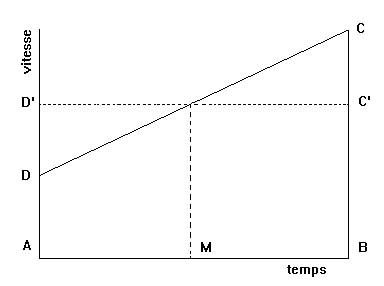
Si M est le milieu de AB, l’aire du trapèze ABCD est égale à celle du rectangle ABC’D’. S’appuyant sur le postulat précédant, notre mathématicien en déduit que la distance parcourue par le mobile dans l’intervalle de temps AB est la même que celle qu’il parcourrait s’il était mu d’une vitesse uniforme égale à celle qu’il possède à l’instant moyen M. Cet énoncé est appelé règle de Merton, du nom d’un collège d’Oxford. Les maîtres de ce lieu l’avaient en effet formulée, mais sans l’appuyer d’une démonstration claire. Nicole Oresme donne ici de cette règle un modèle géométrique facile à appréhender. Une démonstration rigoureuse de ce résultat ne peut se faire qu’en ayant recours au calcul intégral. Jusqu’à l’invention de ce calcul par Cavalieri Fermat et Pascal, deux cent cinquante ans plus tard, la physique n’aura de cette loi du mouvement uniformément accéléré, aucune démonstration meilleure que celle d’Oresme. D’ailleurs ce fameux trapèze fera le tour des universités d’Europe.
Maître Nicole Oresme ne s’arrête pas en si bon chemin. Poursuivant son étude plus avant, il considère un mouvement rectiligne uniformément accéléré dont la vitesse initiale est nulle. Dans ce cas les points A et D du trapèze précédant sont confondus :
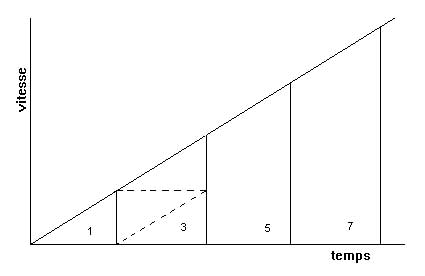
Subdivisant ensuite l’intervalle AB en un certain nombre de parties égales, il fait apparaître clairement sur la figure que les aires des trapèzes au dessus des intervalles sont dans la proportion 1,3,5,7…etc. Il en est donc de même des distances parcourues durant ces intervalles de temps.
«Or, poursuit-il, comme l’a remarqué le grand mathématicien grecque Pythagore, on a :
1 = 1 = 1 fois 1,
1 + 3 = 4 = 2 fois 2,
1 + 3+ 5 = 9 = 3 fois 3,
1 + 3 + 5 + 7 = 16 = 4 fois 4,
1 + 3 + 5 + 7 + 9 = 25 = 5 fois 5,
etc….,
on obtient toujours un nombre carré. Par ce moyen peut-on déterminer les rapports mutuels des quantités totales« (c’est l’expression qu’il emploie pour désigner l’aire).
Nicole Oresme a donc établi la loi fondamentale du mouvement rectiligne uniformément accéléré, à savoir que si la vitesse à l’instant zéro est nulle, la distance parcourue est proportionnelle au carré du temps.
On a coutume de faire de cette loi l’un des titres de gloire du célèbre Galilée. La raison en est que ce grand savant italien a eu l’idée d’utiliser un plan incliné pour vérifier expérimentalement que la loi précédente s’applique au mouvement de la chute d’un corps. L’histoire oublie trop facilement l’apport des maîtres du moyen âge qui ont contribué à enrichir un terreau d’où ont germé nombre d’idées modernes.
Le traité sur les configurations a marqué l’histoire des sciences. La doctrine d’Oresme a été diffusée dans toute l’Europe, en Italie surtout mais aussi à Vienne, Heidelberg et Cologne, comme l’attestent les registres de ces universités. Cependant, lors de l’avènement de l’imprimerie, ce n’est pas le traité original qui fut diffusé, mais une pâle copie1 écrite suivant la doctrine d’Oresme, mais dans laquelle ne figure pas le fameux trapèze. Cet oubli a été réparé grâce à un certain Blasius de Parme. Son livre2 fut amplement diffusé en Italie. Il en résulte que Galilée a certainement eu connaissance de la doctrine d’Oresme à travers ces ouvrages.
De proportionibus proportionum (Proportion de proportion)
Le point de départ de ce traité est une loi de la physique formulée par Thomas Bradwardine (1328) qui reliait de manière compliquée force, résistance et vitesse. Cette loi constituait une première tentative de quantifier la physique d’Aristote. Afin de la formuler en toute généralité Nicole Oresme introduit pour la première fois la notion de puissance d’un nombre d’exposant fractionnaire avec une notation déjà voisine de la notre. Il va même jusqu’à inventer la notion de puissance d’exposant irrationnel en appliquant un principe de continuité. Bien avant l’invention des logarithmes, il affirme qu’étant donnés deux nombres x et y non nuls, il existe toujours un exposant rationnel ou irrationnel e tel que x élevé à la puissance e soit égal à y.
Dans le cas ou x et y sont des nombres entiers il déduit par un raisonnement d’arithmétique élémentaire que la condition pour que l’exposant e soit rationnel est que les décompositions en produit de nombres premiers de x et de y contiennent les mêmes nombres. Il en tire la conclusion que si x et y sont choisis au hasard, il est plus probable que e soit irrationnel plutôt que rationnel. Cela le conduit à penser que lorsqu’un nombre inconnu intervient dans une situation naturelle, il y a de fortes chances que celui-ci soit irrationnel.
Cette remarque est à la base de son argumentation mathématique contre les prédictions astrologiques. Il considère le schéma simple de deux planètes parcourant des orbites circulaires et concentriques avec des vitesses uniformes. Si le rapport des vitesses de rotation des planètes est rationnel, les conjonctions de ces planètes se produiront périodiquement le long d’un nombre fini de rayons (Exactement comme ce qui se passe pour les deux aiguilles d’une horloge, où la grande recouvre la petite tous les onzièmes d’heure). Mais si, ce qui est le plus probable selon la remarque précédente, le rapport des vitesses de rotation des deux planètes est irrationnel, les positions futures des conjonctions dépendent alors des décimales lointaines de ce rapport inconnu des vitesses de rotation. De ce fait ces positions sont impossibles à prévoir à long terme. Ce qui vide de toute substance les affirmations des astrologues.
Même si ces arguments n’ont pas dû ébranlé les astrologues dans leurs convictions, il n’en reste pas moins vrai qu’à cette occasion Nicole Oresme nous dévoile la profondeur de sa pensée mathématique. En particulier concernant l’affirmation de la prépondérance des nombres irrationnels sur les rationnels, il faudra attendre la fin du XIXe siècle pour voir ce résultat clairement précisé et démontré grâce aux travaux de Georg Cantor, le fondateur de la théorie des ensembles.
Œuvres en Français
Traité de la sphère
Il s’agit d’un ouvrage de cosmographie et de géographie où Oresme expose simplement en français ce que lui ont appris sur le système du monde quelques uns des principaux ouvrages de l’antiquité et du moyen âge. En particulier le livre du ciel et du monde d’Aristote dont il donnera plus tard une traduction commentée. Mais aussi un traité de la sphère de Sacrobosco. Voici un aperçu des sujets traités à travers un extrait de la table des matières: «Des sphères célestes, du mouvement des planètes, du zodiaque, de l’inégalité des jours naturels, de la mesure de la terre, de la division de l’habitation de la terre selon aucuns, des causes pourquoi un lieu est habitable ou non, du croissement et appetissement de la lune, des causes des éclipses en général, …»
Le grand intérêt de cette œuvre est de nous montrer l’état des connaissances de cette époque. On lit par exemple que la terre a 15750 lieues de circonférence, que la zone inter tropicale est inhabitable (bien qu’Oresme émette de sérieux doutes à ce sujet), que la zone tempérée antarctique est inhabitée, et que l’hémisphère sud est couvert d’eau. C’est un manuel remarquable pour le temps. C’est d’Oresme que datent les principaux termes d’astronomie, de cosmographie et de géographie employés aujourd’hui pour l’exposition de ces sciences.
Les gloses du traité du ciel et du monde
C’est à la demande formelle du roi que Nicole Oresme va entre 1370 et 1373 traduire du latin en français les œuvres d’Aristote, en particulier un texte du plus haut niveau philosophique: Le traité du ciel et du monde qui va nous apporter une oeuvre d’une importance exceptionnelle pour connaître la pensée de Nicole Oresme. En effet les commentaires (gloses) l’emportent sur le texte traduit et nous révèlent la pensée scientifique de l’auteur. Cette traduction commentée va être rédigée en 1376-77 et valoir comme récompense à Oresme l’évêché de Lisieux le 16 Novembre 1377. En effet à la fin du livre il précise:«Et ainsi à l’aide de Dieu, j’ay accompli le livre du ciel et du monde au commandement de très excellent prince Charles quint de ce nom, par la grâce de Dieu roy de France, lequel en ce faisant m’a fait évesque de Lisieux.»
À la différence de ses traités scientifiques cette œuvre est restée méconnue. Elle n’a pas été imprimée avant l’édition américaine de 1942; on en connaît cinq manuscrits. Dans toutes les gloses du traité Nicole Oresme part du texte d’Aristote dont il accepte l’ensemble de la cosmologie en la rectifiant sur un certain nombre de points. Vis à vis de la tradition il manifeste à la fois un certain respect et une grande liberté critique. Voici les principaux points sur lesquels il se sépare d’Aristote.
Le philosophe grec ignore le principe d’inertie. Pour expliquer la continuation du mouvement d’un projectile après qu’il ait quitté la main du lanceur, il affirme que l’air en s’engouffrant dans le vide créé derrière le projectile par son mouvement, produit un tourbillon qui pousse le corps projeté. Aussi le milieu ambiant est-il indispensable à la continuation du mouvement. Pour Oresme, disciple de Jean Buridan, si la pierre jetée continue son mouvement après avoir quitter la main du lanceur, c’est qu’elle a acquis une qualité motive, qu’il appelle impetus. C’est l’ancêtre de ce que nous appelons l’énergie cinétique.Contre l’argument d’Aristote il considère l’expérience qui consiste à tirer une flèche «fort parmi une faible peau. Elle serait mue bien outre, non obstant que la peau eut arrêté l’air qui la suivait.»
Pour Aristote les orbes célestes qui conduisent les astres sont chacun soumis à un moteur éternel et immuable, intelligence séparée de la matière. Pour Oresme c’est une survivance du paganisme; il propose l’hypothèse que Dieu en les créant a donné à chaque orbe une certaine impulsion qui se conserve naturellement:«quant Dieu créa les cielz, il mist en eulz qualitez et vertus motives aussi comme il mist pesanteur es choses terrestres, et mist en eulz résistances contres ces vertus motives. Et sont ces vertus et ces résistances d’autre nature et d’autre matière que quelconque chose sensible ou qualité qui sont ici-bas. Et sont ces vertus contre ces résistances tellement modérées, attrempées et accordées que les mouvements sont faits sans violence, et excepté la violence, c’est exactement semblable quant un homme a fait une horloge et il la laisse aller être mue continuellement selon les proportions que les vertus motives ont aux résistances et selon l’ordonnance établie…»
Ces idées nouvelles, pour la première fois exprimées en français, il les partage avec l’école de Paris. Mais où il fait preuve d’originalité, c’est quand il formule, dans deux longues gloses qui sont de véritables chapitres, l’hypothèse du mouvement de la terre sur elle-même en vingt-quatre heures. Dans la conception aristotélicienne et scolastique, le monde est constitué d’une immense sphère qui tourne sur elle-même d’orient en occident en entraînant les étoiles fixes; à l’intérieur et à différentes distances du centre, les orbites des planètes et celui du soleil sont aussi entraînés par le mouvement diurne (Oresme dit mouvement journal) de la sphère des fixes; mais les planètes, la lune et le soleil se déplacent par rapport à la sphère des fixes dans le sens inverse du mouvement diurne, selon un axe incliné par rapport à l’axe des pôles célestes. Aristote affirme que, au centre de ce système de sphères et de cercles homocentriques, la terre doit nécessairement rester immobile. Ce dispositif correspond aux apparences et semble en accord avec l’expérience.
Oresme ne met pas en cause la forme sphérique du monde, ni le géocentrisme; il propose seulement d’expliquer le mouvement diurne par l’hypothèse de la rotation de la terre sur elle-même par rapport à l’ensemble du ciel immobile, et il montre que les deux hypothèses sont équivalentes. Mais il ajoute ensuite, en faveur de son hypothèse de «belles persuasions» qui lui donnent la priorité.
Pour soutenir l’équivalence des deux hypothèses il rappelle que l’expérience nous montre qu’il y a des illusions au sujet du mouvement: soit deux nefs A et B immobiles, si je suis sur A, n’ayant aucun autre repère que B, et si A se met en mouvement j’ai l’impression que B se déplace et que je suis immobile. «et semblablement, si un homme était au ciel, posé qu’il soit mu de mouvement journal, et que cet homme qui est porté avec le ciel voit clairement la terre et distinctement les mons, les vauls, les fleuves, villes et châteaux, il lui semblerait que la terre fut mue de mouvement journal, aussi comme il semble du ciel à nous qui sommes à terre. Et semblablement si la terre était mue de mouvement journal et le ciel non, il nous semblerait que la terre reposast et que le ciel fust mu; et ce peut imaginer légèrement (facilement) chacun qui a bon entendement».
Voici, parmi d’autres, quelques arguments qui font pencher en faveur du mouvement de la terre: d’une part, c’est la chose qui a besoin d’une autre chose qui se meut pour recevoir le bien qu’elle en attent ; «et donc la terre et les éléments de cy-bas qui ont mestier (besoin) de la chaleur et de l’influence du ciel tout environ, doivent êtres disposés par leur mouvement à recevoir ce profit dûment. Ainsi à parler familièrement, comme la chose qui est rôtie au feu reçoit environ elle la chaleur du feu pour ce qu’elle est tournée, et non pas pour ce que le feu soit tourné environ elle.» D’autre part, étant donné l’immensité de la sphère céleste, et la vitesse inimaginable qu’elle aurait pour tourner en vingt-quatre heures, il est plus raisonnable de supposer le mouvement de la terre. De plus Aristote dit que Dieu et la nature ne font rien en vain. Il est donc plus simple, pour expliquer les mêmes effets, de supposer le mouvement de la terre plutôt que celui du ciel.
Ecrit en français, sur l’ordre du roi, à ses frais, par un personnage les plus considérables de l’université de Paris, le commentaire du Traité du ciel et du monde composé par Maître Nicole Oresme dut jouir en France d’une grande vogue. En revanche, le fait même qu’il ait été rédigé en français dut empêcher qu’il fut aisément connu dans les universités étrangères. Au début du XVIe siècle, l’imprimerie française publia les autres traductions faites par Oresme, celle des Ethiques comme celle des Politiques et des Économiques ; elle donna aussi, et par deux fois le Traité de la sphère que les manuscrits joignent souvent au Traité du ciel et du monde, conformément au désir qu’ Oresme lui-même avait exprimé; chose étrange, la presse délaissa le seul Traité du ciel et du monde. De ce fait, Pierre Duhem doute fort que Nicolas Copernic ait eu connaissance de cet écrit. Pourtant, poursuit l’historien des sciences, en lisant ce que Copernic a écrit pour établir la possibilité et la vraisemblance du mouvement diurne de la terre, on est frappé des analogies qui rapprochent la pensée du chanoine de Thorn de celle de l’évêque de Lisieux.
Conclusion
Nicole Oresme a eu une carrière brillante due à sa valeur et à son travail. Il a reçu bien des honneurs qu’il méritait. Il a honoré et perfectionné la langue française. Son rôle dans le passage de la science médiévale à la science moderne a eu une importance capitale; parmi ses contemporains de l’école de Paris qui ont soutenu les mêmes innovations, il est celui qui, par le style et en esprit, a été le plus proche de la science moderne.
Bibliographie
1 — Meunier Francis. — Essai sur la vie et les ouvrages de Nicole Oresme. — Paris 1857.
2 — Louise Gilbert. — Un grand scolastique normand: Nicole Oresme. — Annuaire des cinq départements de la Normandie. Congrés de Bayeux 1982, p.117-125.
3 — Duhem Pierre. — Un précurseur français de Copernic: Nicole Oresme (1377). — Paris 1909.
4 — Duhem Pierre. — Le système du monde (vol.7 et 8: La physique parisienne au 14e siècle). — Paris 1954.
5 — De Fréville Ernest. — Mémoire sur la cosmographie du moyen âge. Le traité de la sphère par Nicolas Oresme et les découvertes maritimes des normands. — Revue des sociétés savantes des départements, Deuxième série, Il,(1859),pp. 705-29.
6 — Grant Eward. — Nicole Oresme De proportionibus proportionum and Ad pauca respicientes. — The university of Wisconsin press Madison 1966.
7 — Clagett Marshall. — The science of Mechanic in the Middle Ages. — The university of Wisconsin press Madison 1959.
8 — Clagett Marshall. — Nicole Oresme and the Medieval Geometry of Qualities and Motions. A treatise on the uniformity and difformity of intensities known as Tractatus de configurationibus qualitatum et motuum. — The University of Wisconsin press Madison 1968.
9 — D.Menut Albert and J.Denomy.C.S.B. — Maistre Nicole Oresme Le livre du Ciel et du Monde. Text and Commentary. — Medieval studies Vol. 3-5 (1941-43).
10-Bourbaki Nicolas — Eléments d’histoire des mathématiques — Hermann. Paris.1969.
11 — Boyer C.D. Merszbach.U.C. — History of mathematic. — John Wiley 1991.
12 — Taton René. — Histoire générale des sciences. — Presses universitaires de France 1957.


